“The behavior of things in the small scale is so fantastic! It is so wonderfully different! So marvelously different than anything that behaves on a large scale.” – Feynman
Here you will find descriptions of my current and past research, illustrated with images, slides, posters, and animations. To skip directly to publications, see below here or go to arXiv or ORCID.
Available positions
Genuinely motivated undergraduate or masters students interested in a research project (three months minimum at RRI) within the Visiting Student Program are welcome to contact me at shovan.dutta@rri.res.in — please note that I may not always be able to reply due to the large number of applications, particularly for summer internships. Interested PhD candidates please see the institute portal (usually opens in March). There may also be very few postdoc positions.
Brief bio
Assistant Professor, Raman Research Institute, 2022 – present [TP webpage]
Guest Scientist, Max Planck Institute for the Physics of Complex Systems, 2021 – 2022
Research Associate, University of Cambridge, 2018 – 2021 [TCM webpage]
PhD Physics, Cornell University, 2018
BE, Jadavpur University, 2012
Overview
Physics speak
My research is focused on uncovering collective properties of interacting quantum gases by theoretical modeling and numerical simulation. This is in part motivated by a remarkable growth of versatile experimental platforms for trapping and manipulating atoms and photons. My recent work has explored novel quantum states and dynamics arising in the presence of symmetry, dissipation, and external fields, as well as developing efficient many-body approaches such as the DMRG. I am also interested in how classical nonlinear phenomena, such as limit cycles, chaos, turbulence, etc., emerge from a quantum description. I play with ideas from condensed matter, quantum optics, quantum information, and nonlinear dynamics. I am drawn to simple, concrete, visually appealing models that highlight general physical principles.
In plain English
I play with the mathematical rules of quantum mechanics to explore the wonderfully strange small-scale behavior in Feynman’s quote above. Although everything is made up of these tiny objects or “atoms,” their quantum nature is often blurred by thermal fluctuations (random jiggling motion). As matter is cooled down, these fluctuations die out and one enters the quantum realm in full glory. Thanks to experimental advances, it is now possible to “cook” such scenarios in the lab and “look” at how individual particles behave. Understanding this quantum world is central to modern electronics and will play a key role in future technologies. I use a blend of analytical and numerical approaches to explore the rich collective features that emerge in these systems. For example, below are some news articles written for a general audience.
- Mutating Quantum Particles Set in Motion
- Towards table-top quantum simulation of vacuum decay
- Hidden symmetry could be key to more robust quantum systems, researchers find
- A quantum ear
- Researchers pave an enlightened path to anyons and quantum computation
- Surprising nature of quantum solitary waves revealed
Publications
- G Preethi and Shovan Dutta, “Frustrated Quantum Magnetism on Complex Networks: What Sets the Total Spin,” arXiv:2403.09116 [pdf] [slides] [ICTS talk].
Click here to read more!
In solid-state physics we typically learn about systems with short-range interactions on a regular lattice. However, in the past two decades a growing number of interdisciplinary studies have looked at complex networks of dynamical units, finding that the network topology itself can radically alter collective dynamics such as disease spreading and give rise to new phenomena such as explosive synchronization. However, most of these studies are limited to classical systems, e.g., social networks. There is no general understanding of how network structure governs collective quantum phenomena, especially in frustrated systems. Frustration arises when the bonds of a network cannot all be satisfied, the simplest example being a triangle of spins where each bond wants to anti-align the spins at its two ends. Such frustrated magnets are actively studied on lattices, where they lead to exotic phases of matter such as a quantum spin liquid.
Here we explore what happens on more general networks with equal antiferromagnetic (Heisenberg) bonds that can encode arbitrary levels of frustration. Specifically, we ask: What property of the network determines the net magnetization and how tunable is it? By systematically examining various network families we deduce that (i) heterogeneity in the number of neighbors (degree) is essential for nonzero total spin, (ii) surprisingly, the total spin is not sensitive to the frustration level, (iii) instead, it can be tuned over almost its entire range by embedding “hubs” connected to many low-degree nodes. We also describe a simple network where the magnetization can be tuned by varying some of the bond strengths. These findings raise a number of fundamental questions that can be probed on existing platforms (e.g. trapped ions) and strongly encourage wider exploration of quantum many-body physics beyond regular lattices.
- Shovan Kanti Barik, Silpa B S, M Venkat Ramana, Shovan Dutta, and Sanjukta Roy, “Doppler-enhanced quantum magnetometry with thermal Rydberg atoms,” arXiv:2308.05190 [pdf].
Click here to read more!
Precise measurement of magnetic fields has a wide variety of applications, from brain imaging to space explorations. Quantum effects in trapped atomic gases provide a powerful tool to sense weak magnetic fields. However, at room temperature Doppler shifts arising from the irregular motion of atoms broaden the measured signal, posing a significant hindrance. Here we show how one can actually harness Doppler shifts by using laser beams in an unconventional configuration. We experimentally demonstrate that the magnetic-field response can be enhanced by an order of magnitude compared to usual setups.
We pump Rubidium atoms to a highly excited energy level, called a Rydberg level, using a “probe” laser and a “coupling” laser addressing two atomic transitions and overlapping with each other through the atomic vapor. At resonances quantum effects cancel the absorption of the probe beam, rendering the vapor transparent and producing transmission peaks in the output, which is known as Electromagnetically Induced Transparency. We show that by using copropagating lasers the splitting between the peaks is greatly amplified compared to the traditional counterpropagating arrangement. We perform theoretical modeling to explain and generalize our measurements.
- Sayak Bhattacharjee, Roderich Moessner, and Shovan Dutta, “Density-and-phase domain walls in a condensate with dynamical gauge potential,” arXiv:2212.14195 [pdf].
Click here to read more!
Interacting matter and gauge (force) fields play a fundamental role in physics, from the Standard Model to classical electromagnetism. Thus, a lot of effort has been devoted to simulating such fields in engineered platforms, e.g., with cold atoms in optical lattices. As a key step, recent experiments have realized artificial gauge fields that vary dynamically with the local matter density. Although not independent of matter, these gauge fields already introduce a nonlinearity that can give rise to exotic collective structures.
Here we show how one can apply a density-dependent gauge field to a Bose-Einstein condensate to create domain walls in the ground state where the density falls sharply and the momentum switches sign. The gauge potential gives rise to synthetic electromagnetic fields that are localized at the domain wall, reminiscent of flux-attached particles. Furthermore, At strong fields the domain wall can suddenly disappear across a first-order transition that ends at a critical point. These results strongly motivate future studies into the dynamics and metastability of such domain walls.
- Shovan Dutta, Stefan Kuhr, and Nigel R. Cooper, “Generating symmetry-protected long-range entanglement,” Phys. Rev. Research (Letter) 6, L012039 (2024) [pdf] [arXiv] [slides].
Click here to read more!
Entanglement and non-locality are two of the most iconic and counterintuitive predictions of quantum mechanics, with far-reaching applications in quantum technologies. Two quantum bits (qubits or spins) are “entangled” when their states are inseparable from one another, and measuring one immediately affects the other, even though they are spatially far apart. Experiments can nowadays maximally entangle two isolated qubits over over distances. However, when many of them interact with one another, creating such long-range entanglement has proved very challenging.
We introduce a simple yet general technique that harnesses the existence of a symmetry to produce entanglement over increasingly longer distances. In particular, we show how one can efficiently generate any target number of distant yet maximally-entangled pairs of qubits (“Bell pairs”) using timed local pulses, which can be realized on several experimental platforms. More generally, our approach provides a way to prepare exotic quantum correlations not accessible by conventional methods. For example, it allows one to create a long-sought-after superconducting state (η pairs) of repulsively interacting fermions.
- Shovan Dutta, Anton Buyskikh, Andrew J. Daley, and Erich J. Mueller, “Density-Matrix Renormalization Group for Continuous Quantum Systems,” Phys. Rev. Lett. 128, 230401 (2022) [pdf] [supplement] [arXiv] [TCM highlight] [slides] [15-min talk] [Code].
Click here to read more!
What prohibits a classical simulation of large quantum systems is that the number of all possible states grows exponentially with the system size. For discrete/lattice systems, the “Density-Matrix Renormalization Group” (DMRG) technique provides a solution by letting one truncate this space based on the entanglement between subsystems. Indeed, DMRG is the state of the art for simulating such systems. However, extending DMRG to continuous systems has proved elusive, particularly for inhomomgeneous or time-dependent settings. We introduce a new versatile approach that can overcome this long-standing challenge.
We divide space to map a continuous many-body Hamiltonian to a discrete sum over segments, each with a flexible set of basis functions. By combining this mapping with traditional DMRG routines, we show how one can accurately obtain physical quantities directly in the continuum, demonstrating fast convergence for both homogeneous and inhomogeneous settings. Our approach can be tailored to a wide variety of physical systems and opens up DMRG and tensor networks for tackling challenging problems in the continuum. Our open-source code can be found at github.com/Shovan-Physics/cDMRG.
- Bo Song, Shovan Dutta, Shaurya Bhave, Jr-Chiun Yu, Edward Carter, Nigel Cooper, and Ulrich Schneider, “Realizing discontinuous quantum phase transitions in a strongly-correlated driven optical lattice,” Nature Physics 18, 259 (2022) [pdf] [supplement] [arXiv] [Cavendish press] [Cavendish Magazine] [TCM highlight] [Physics World] [Nature Physics News & Views] [slides].
Click here to read more!
We have all seen wine glasses being shattered by a high pitch! The resonant sound excites increasingly strong vibrations until the glass order is broken. Here we realize a quantum phase transition where one can resonantly shake an insulator and turn it into a superfluid. We trap strongly-interacting ultracold atoms in a 1D optical lattice formed by standing waves of a laser. Modulating the laser frequency shakes the lattice, coupling the lowest energy bands and driving the novel phase transition. For weak shaking, this transition is discontinuous and the atoms can be stuck in the insulating state, whereas for strong shaking, they undergo a continuous transition toward a π-superfluid. This tunable quantum metastability and hysteresis are in good agreement with theoretical (DMRG) predictions and pave the way for understanding the crucial role of quantum fluctuations in the emergence of spatial structures from discontinuous phase transitions, such as in the inflationary early universe.
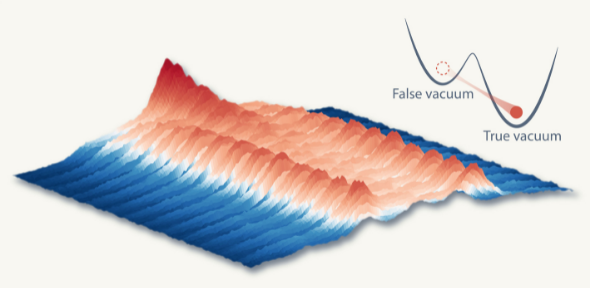
- Liam L.H. Lau and Shovan Dutta, “Quantum walk of two anyons across a statistical boundary,” Phys. Rev. Research (Letter) 4, L012007 (2022) [pdf] [supplement] [arXiv] [Cavendish press] [TCM highlight].
Click here to read more!
Fundamental particles come in two varieties: fermions or “matter particles” and bosons or the “force carriers.” Remarkably, what sets them apart is how the overall quantum state is affected when two particles are exchanged. This “exchange statistics” is what gives rise to the periodic table of elements with fermions and solar radiation with bosons. It also distinguishes how two particles walk on a lattice: bosons tend to move together, or bunch, whereas fermions tend to move in opposite directions, or antibunch.
We introduce the idea of a statistical boundary where particles can effectively change their exchange statistics by hopping across a domain wall in a 1D lattice. Such a domain wall is invisible to single particles and affects the physics only by swapping two particles in its vicinity. We show the bunching or antibunching is dramatically altered in the presence of such an interface. In particular, bunched particles incident from one side can get completely reflected or split into a bunched and antibunched wave, leading to striking phenomena such as trapping or fragmentation. We show this novel setup can be realized in present-day atomic setups. Our findings open up a new class of inherently many-particle dynamics at statistical interfaces.
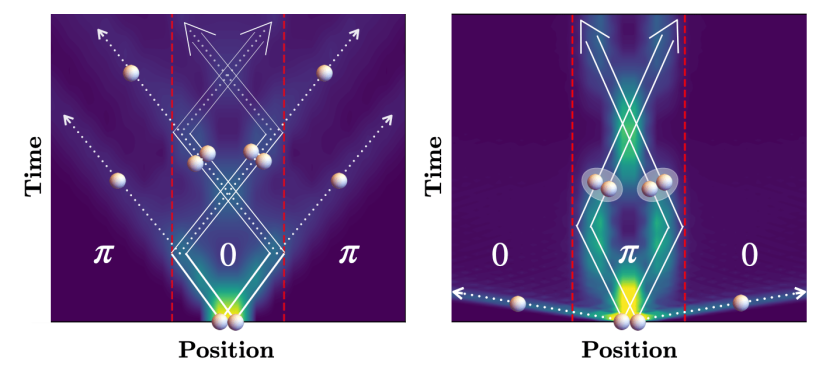
- Shovan Dutta and Nigel R. Cooper, “Out-of-equilibrium steady states of a locally driven lossy qubit array,” Phys. Rev. Research (Letter) 3, L012016 (2021) [pdf] [supplement] [arXiv].
Click here to read more!
Motivated by our previous work (see below), we characterize the steady states of a qubit array coupled to a source and a sink at two generic sites. We find a rich variety of counterintuitive features, including dissipation-induced long-range coherence and a striking density-wave order in a class of resonant geometries. Our findings are accssible in existing setups and differ significantly from the steady states found before in special cases. We develop general methods for approximating the long-time dynamics, finding key physical principles that strongly motivate studies of nonequilibrium phases through engineered pump and loss.
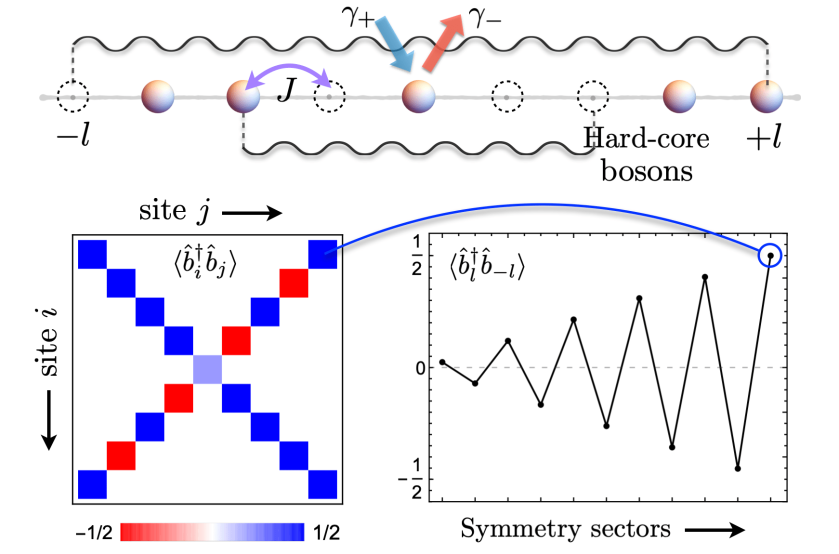
- Shovan Dutta and Nigel R. Cooper, “Long-Range Coherence and Multiple Steady States in a Lossy Qubit Array,” Phys. Rev. Lett. 125, 240404 (2020) [pdf] [supplement] [arXiv] [Cambridge press] [TCM highlight] [slides] [poster] [10-min talk] [TIFR seminar] [PCTS seminar].
Click here to read more!
Environmental coupling typically drives a quantum system to a unique steady state with very little coherence, which is a major obstacle for quantum control and information processing. Here we identify a simple experimental setting of two-level systems with local pump and loss that can stabilize multiple highly coherent steady states. These states arise from a hidden symmetry that conserves entangled particle-hole pairs over arbitrarily long distances, giving rise to controllable long-range entanglement. We show how to selectively prepare and observe the steady states in existing setups. Our conclusions apply to a broad range of two-level quantum systems.
- Shovan Dutta and Nigel R. Cooper, “Critical Response of a Quantum van der Pol Oscillator,” Phys. Rev. Lett. 123, 250401 (2019) [pdf] [arXiv] [TCM highlight] [slides] [poster].
Click here to read more!
Self-sustained oscillations are ubiquitous in nature, from heartbeats to electrical circuits. Physical systems on the verge of such oscillations are incredibly sensitive to external drives and play a key role in biological sensors. For example, this is how we can hear faint whispers (see the power of hearing). In this work, we find this heightened sensitivity persists even in the microscopic world of atoms and photons, where the disparate rules of quantum mechanics dominate. An actively driven quantum oscillator not only shows enhanced sensitivity, but also exhibits surprising new features that are unique to the quantum realm. These findings could have important applications in quantum sensing and shed new insights into the out-of-equilibrium dynamics of quantum systems.
We model a prototypical scenario where a quantum oscillator is subject to energy dissipation. Ordinarily, the response of such oscillators is limited by damping. However, we find this limit can be negated via a strong “pump,” leading to enhanced sensitivity. Additionally, the study reveals novel features such as a regime where the response diminishes with increasing drive. These predictions can be tested in a variety of setups, e.g., atoms trapped in a well, light in a cavity, or a micromechanical membrane. Such platforms have already been used to build quantum sensors that are transforming the landscape of precision metrology and medical imaging (see https://www.bbc.co.uk/news/business-47294704). Active sensing could promote further advances, yielding a “quantum ear” that can detect ultraweak signals.
- Shovan Dutta and Erich J. Mueller, “Coherent generation of photonic fractional quantum Hall states in a cavity and the search for anyonic quasiparticles,” Phys. Rev. A 97, 033825 (2018) [pdf] [supplement] [arXiv] [Cornell press] [slides1] [slides2] [poster] [animation].
Click here to read more!
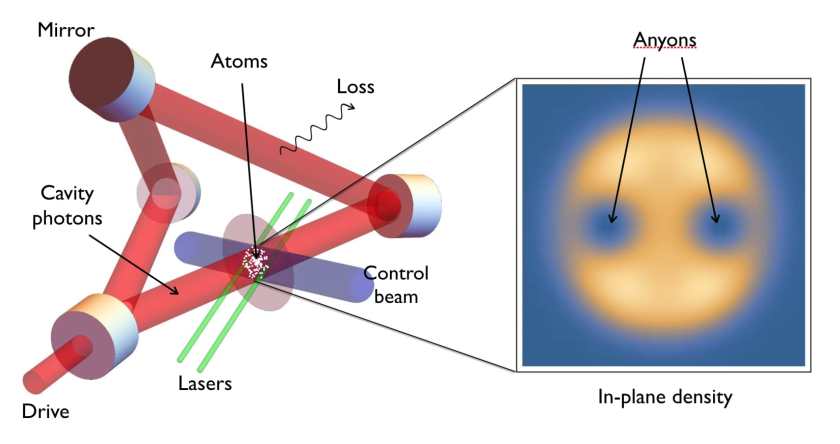
Wave-particle duality is a key principle of quantum mechanics. Central to modern electronics, it explains that matter has dual nature: “particles” like electrons can act as waves and “waves” like light can act as particles. Following new lines of research which build on this concept, we model an experimental setting where the particles of light (photons) can mimic a very special behavior of electrons in semiconductors. In particular, we show how one can use light in a cavity to create and manipulate exotic quantum excitations, known as anyons, which could form the hardware for future quantum computers. This protocol might enable the first direct probe of these exotic entities which have remained elusive.
In the protocol, the anyons are formed in the waist of an optical cavity built by carefully aligning a set of high-quality mirrors. Such a setup already exists in Jon Simon’s lab in Chicago. We show how one can drive the cavity with lasers to sequentially inject photons, building up a quantum state which has vortex-like excitations with unusual properties. These excitations are the desired anyons: they act like particles, but due to their collective nature behave unlike any known elementary particle. In particular, when two of them are exchanged, the quantum-mechanical wavefunction gains a fractional phase. We explain how one use laser beams to create and move these anyons, and measure the fractional phase. The proposed experiment uses existing technology and can be considered the simplest “braiding” protocol, which forms the basis of topological quantum computing schemes.
- Shovan Dutta and Erich J. Mueller, “Protocol to engineer Fulde-Ferrell-Larkin-Ovchinnikov states in a cold Fermi gas,” Phys. Rev. A 96, 023612 (2017) [pdf] [arXiv].
Click here to read more!
Following up on our result in the previous paper (see below), here we propose a two-step experimental protocol to directly engineer FFLO states in a cold Fermi gas loaded into a quasi-1D trap. First, one uses phase imprinting to generate a series of domain walls in a superfluid with equal number of ↑- and ↓-spins. Second, one applies a controlled radio-frequency sweep which selectively breaks Cooper pairs near the domain walls and transfers the ↑-spins to a third noninteracting spin state, leaving behind a stable FFLO state with one unpaired ↓-spin in each domain wall. We show how the protocol can be implemented with high fidelity for a wide range of parameters available in experiments.
- Shovan Dutta and Erich J. Mueller, “Collective Modes of a Soliton Train in a Fermi Superfluid,” Phys. Rev. Lett. 118, 260402 (2017) [pdf] [arXiv] [Cornell press] [slides] [poster].
Click here to read more!
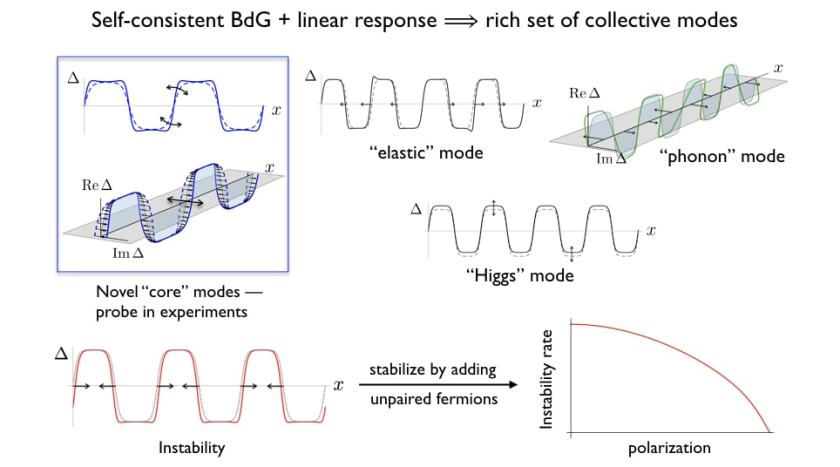
We study the collective motion of a train of domain walls or solitons in a quasi-1D Fermi superfluid by analyzing the Bogoliubov-de Gennes equations. We uncover a variety of unexpected modes, including long-lived gapped modes describing oscillations of the soliton cores and an instability where pairs of solitons collide and annihilate. The instability rate is sensitive to the separation of solitons and the interaction between atoms, both of which can be tuned in experiments. In addition, the instability is prevented by magnetizing the gas – forming an exotic FFLO state which has eluded direct experimental detection despite much effort over decades. We discuss how such stable FFLO states can be directly engineered in cold Fermi gases.
- Shovan Dutta and Erich J. Mueller, “Dimensional crossover in a spin-imbalanced Fermi gas,” Phys. Rev. A 94, 063627 (2016) [pdf] [arXiv] [slides].
Click here to read more!
We study the relative stability of exotic superfluid states, such as the FFLO and breached-pair states, in a spin-imbalanced Fermi gas confined in a cylindrical harmonic trap. We calculate the mean-field phase diagram in the density–imbalance plane as a function of the confinement, strength of interactions between atoms, and temperature. The phase diagram changes from 1D-like to 3D-like as one increases the interactions or reduces the confinement. We map the system to an effective 1D model, finding significant density dependence of the 1D scattering length. We discuss the prospects of observing the superfluid states in similar ongoing experiments.
- Shovan Dutta and Erich J. Mueller, “Kinetics of Bose-Einstein condensation in a dimple potential,” Phys. Rev. A 91, 013601 (2015) [pdf] [arXiv] [slides].
Click here to read more!
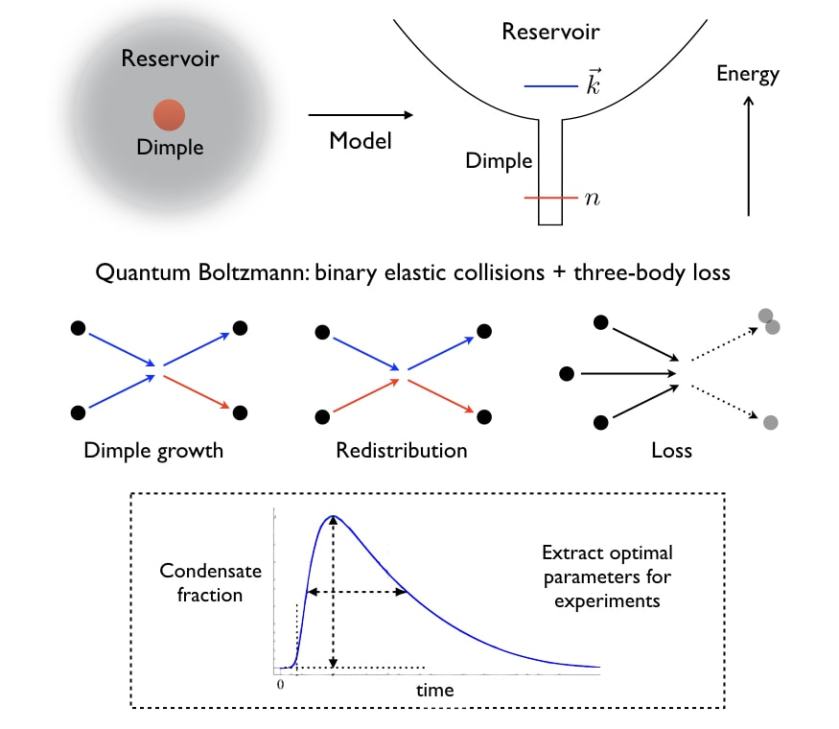
We model the dynamics of condensate formation in a bimodal optical trap, consisting of a large reservoir region and a tight, tunable “dimple” potential at the center. We simulate the quantum Boltzmann rate equations with two-body scattering and three-body loss processes to provide detailed quantitative estimates for condensate yields, lifetimes, thermalization timescales, and temperature variations. We study the dependence of these quantities with the trap parameters, explaining the principal trends in physical terms and extracting optimal parameters for future experiments.
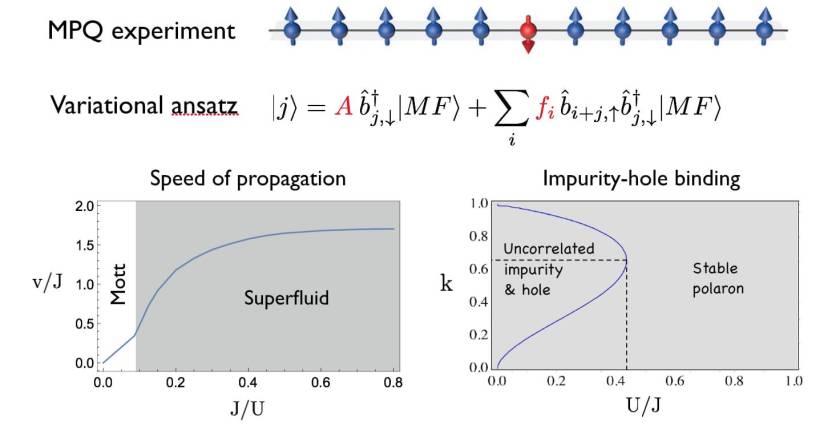
- Shovan Dutta and Erich J. Mueller, “Variational study of polarons and bipolarons in a one-dimensional Bose lattice gas in both the superfluid and the Mott-insulator regimes,” Phys. Rev. A 88, 053601 (2013) [pdf] [arXiv] [slides].
Click here to read more!
We model the spread of an impurity in a 1D Bose gas across the Superfluid-Mott transition through a computationally tractable variational ansatz. When the interactions between atoms are strong, we find the impurity binds with a hole, forming a quasiparticle known as a polaron. We characterize the dynamics and stability of this polaron and explain the features observed in a recent experiment. We find that two polarons can bind together to form a bipolaron. At weaker interactions, the polaron becomes unstable over a growing range of momentum and decays into particle-hole excitations. We predict how this instability can be observed in experiments by measuring the impurity-hole correlation.
E-prints
- Shovan Dutta, “Collective Phenomena in Quantum Gases,” PhD thesis (2018).
Click here to read more!
Motivated by rapid experimental progress in the fields of ultracold atoms and quantum optics, I present a series of theoretical studies which explore collective phenomena in quantum gases of atoms and photons. In Chapter 1, I highlight the major developments in the research field and identify the overarching themes and motivations. I also provide a roadmap for the rest of the thesis and summarize the main results. The remaining eight chapters contain original studies, organized along three broad motifs. In Chapters 2 through 5, I investigate how the nature of collective excitations and quasiparticles can be explored in modern experiments. More specifically, I model the dynamics of a spin impurity in a Bose lattice gas, develop a protocol for observing fractionalized excitations or anyons in an optical cavity, and characterize the collective dynamics of Bogoliubov quasiparticles and domain walls in a Fermi superfluid. In Chapters 6 and 7, I examine unconventional superfluid phases in spin-imbalanced Fermi gases. In particular, I propose a novel technique for engineering the long-sought-after Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) phase and study the relative stability of exotic phases across a dimensional crossover. Finally, Chapters 8 and 9 are devoted to studies of kinetics in out-of-equilibrium systems. I model the formation of a Bose-Einstein condensate in a dimple trap and characterize the approach to thermal equilibrium in quasi-one-dimensional geometries.
- Shovan Dutta and Subhankar Ray, “Damped bead on a rotating circular hoop – a bifurcation zoo,” arXiv:1201.1218 (2012) [slides].
Click here to read more!
We investigate the evergreen problem of bead on a rotating hoop, but with damping. The introduction of damping alters the nature of the fixed points, giving rise to a multitude of new bifurcations. We show phase portraits and trajectories corresponding to different motions of the bead, characterizing its dynamics over the full parameter space. For certain critical values of the damping coefficient and rotation speed, linear stability analysis is insufficient to classify the nature of the fixed points. We present a rigorous technique involving transformation of coordinates and order of magnitude arguments to resolve such cases, which might provide a general framework to treat such borderline cases in more complex nonlinear systems.
- Shovan Dutta and Subhankar Ray, “Bead on a rotating circular hoop: a simple yet feature-rich dynamical system,” arXiv:1112.4697 (2011).
Click here to read more!
We perform an in-depth analysis of the nonlinear dynamics of an undamped bead on a rotating hoop using elementary calculus and symmetry arguments. We characterize the different types of motion the bead can undergo and show simulations of its beautiful trajectories. At a critical rotation speed, the system undergoes a pitchfork bifurcation where two new equilibrium points emerge on either side of the hoop. We find a dramatic change in the relation between time period and amplitude of bead oscillations as the rotation speed is varied. The study would be particularly useful to students as it illustrates such concepts as phase portraits, bifurcations, symmetry breaking, critical slowing down, and the use of Lagrange multipliers to determine constraint forces.
- Shovan Dutta, Subhankar Ray, and J. Shamanna, “Continuous Time Random Walk with time-dependent jump probability: a direct probabilistic approach,” arXiv:1112.3253 (2011).
Click here to read more!
We tackle the problem of a continuous-time random walk in 3D under time-varying external fields: the random walker, on arriving at position ρ at time τ, stays there for a time t´, after which it jumps to a new position at time t = τ + t´. The waiting time t´ is distributed with a probability density function ψ(t´). The probability that a jump occurring at time t results in a displacement between r´ and r´ + dr´ is φ(r´|t) d3r´. The goal is to find the probability density p(r,t) that the random walker is at position r at time t. Continuous-time random walks are good models of anomalous diffusion.
We use direct probability arguments to derive recurrence relations for all moments of p(r,t) for arbitrary choices of ψ(t´) and φ(r´|t). For a memoryless walk, where ψ(t´) is exponential, we simplify these equations further to find a closed form expression for p(r,t). We also consider the special case of a 1D lattice with nearest-neighbor jumps, which was modeled in prior work by a Fractional Fokker-Planck Equation (FFPE). Our equations reproduce the mean and standard deviation in the FFPE formulation but has additional terms for the higher moments which can markedly alter the asymmetry (skewness) and peakedness (kurtosis) of p(r,t). We show that the missing terms are an artifact of the approximation in taking the continuum limit to derive the FFPE.
- Shovan Dutta, “A simple circuit model showing feature-rich Bogdanov-Takens bifurcation,” IEEE link [best paper in National Students Paper and Circuit Design Contest (NSPCDC) 2011].
Click here to read more!
I propose an easy-to-implement circuit model for the Bogdanov-Takens bifurcation, exhibiting three local (spiral-to-node, saddle-node, Andronov-Hopf) and one global (Homoclinic) bifurcations. The bifurcations have a profound effect on the system stability. For example, in the Homoclinic bifurcation, a stable limit cycle collides with a saddle and disappears. Thus the physical variables such as currents and voltages executing sustained oscillations suddenly increase in an unbounded manner. Such dramatic changes are useful in describing voltage collapse in power systems, excitability of neurons, and several other phenomena. With the proposed circuit, one can experimentally measure the drastic changes in the dynamics simply by altering the values of some linear circuit elements.
Talks
- 2024
- (Invited) “Frustrated quantum magnetism on complex networks,” Stability of Quantum Matter in and out of Equilibrium at Various Scales (SQMVS-2024), ICTS, January 19, 2024 [slides] [YouTube].
- 2023
- (Invited) “Frustrated quantum magnetism on complex networks,” Annual Conference on Quantum Condensed Matter (QMAT-23), NISER Bhuvaneswar, November 28, 2023.
- (Invited) “Ergodicity breaking in kinetically constrained open quantum systems,” Emerging Topics in Quantum Technology (ETQT-23), IIT Palakkad, November 3, 2023.
- “Emergence of classical limit cycle and algebraic relaxation from a Markovian open quantum system,” CMD Seminar, MPIPKS, Germany, April 27, 2023.
- (Invited) “Long-range multipartite entanglement with local drive,” Physics Seminar, Institute of Mathematical Sciences (IMSc), Chennai, March 13, 2023.
- “Multipartite entanglement from local drive,” 8th Indian Statistical Physics Community Meeting (ISPCM’23), ICTS, Bangalore, February 2, 2023.
- 2022
- “Producing maximal long-range entanglement in qubit arrays,” New trends in Nonequilibrium Many-Body Systems: Methods and Concepts (NEQMBS22), MPIPKS, Germany, August 2, 2022.
- “Entangled quantum bits protected by symmetry,” Talk for visiting undergraduates, MPIPKS, Germany, July 13, 2022.
- “Mapping spins to fermions: how one gets entanglement from loss,” Condensed Matter for Dummies (CMD), MPIPKS, Germany, June 24, 2022.
- “Symmetry-protected long-range entanglement qubit arrays,” Condensed Matter Seminar, MPIPKS, Germany, June 23, 2022.
- (Invited) “Long-range entanglement in lossy qubit arrays,” Open System Control of Atomic and Photonic Matter (OSCAR), Bad Honnef, Germany, June 15, 2022.
- “Controllable long-range entanglement in a lossy qubit array,” Physical Research Laboratory (PRL) Seminar (online), April 4, 2022.
- “Controllable long-range entanglement in a lossy qubit array,” S. N. Bose National Centre for Basic Sciences (SNBNCBS) Seminar (online), February 14, 2022.
- “Hidden symmetry and long-range entanglement in a lossy quantum system,” Tata Institute of Fundamental Research Hyderabad (TIFR-H) Seminar (online), January 17, 2022.
- “Controllable long-range entanglement in a lossy qubit array,” Raman Research Institute (RRI) Seminar (online), January 10, 2022.
- 2021
- “Using DMRG to probe tuneable phase transitions in a shaken lattice and extending to the continuum,” Harish-Chandra Research Institute (HRI) Condensed Matter Seminar (online), November 30, 2021.
- “Controllable long-range entanglement in a lossy qubit array,” Indian Association for the Cultivation of Science (IACS) Condensed Matter Seminar (online), November 26, 2021.
- “Controllable long-range entanglement in a lossy qubit array,” Harish-Chandra Research Institute (HRI) Physics Colloquium (online), November 22, 2021.
- (Invited) “Hidden symmetry and long-range entanglement in a lossy qubit array,” Quantum Optics Group Meeting (online), University of Liège, November 15, 2021.
- “Pulsed Generation of Symmetry-Protected Long-Range Entanglement,” Collective Phenomena Group Meeting (CPGM) (online), October 12, 2021.
- “DMRG for Continuous Systems,” Condensed Matter and Quantum Materials (CMQM 2021) Conference (online), June 22, 2021 [YouTube].
- (Invited) “Hysteretic quantum phase transitions in a strongly-correlated driven optical lattice,” Physics of Quantum Materials Discussion Group (online), University of Kent, June 14, 2021.
- “Hysteretic quantum phase transitions in a strongly-correlated resonantly driven optical lattice,” Seminar (online), International Centre for Theoretical Sciences (ICTS), Bangalore, April 27, 2021.
- “Density Matrix Renormalisation Group for Continuous Systems,” Korrelationstage 2021 (online), Max Planck Institute for the Physics of Complex Systems, Dresden, April 15, 2021.
- (Invited) “Long-range entanglement and multiple steady states in a lossy qubit array,” Theoretical Physics Seminar (online), University of Birmingham, March 25, 2021.
- “Out-of-Equilibrium Steady States of Driven Lossy Qubit Arrays,” Many Body Physics in Open Quantum Systems Meeting (online), Princeton Center for Theoretical Science (PCTS), Princeton NJ, January 29, 2021 [Zoom video].
- “Long-range entanglement and multiple steady states in a lossy qubit array,” Statistical Physics Journal Club (online), International Centre for Theoretical Sciences (ICTS), Bangalore, January 7, 2021.
- 2020
- “Long-range entanglement and multiple steady states in a lossy qubit array,” Random Interactions Seminar (online), Tata Institute of Fundamental Research (TIFR), Mumbai, November 26, 2020 [YouTube].
- “Long-range entanglement and multiple steady states in a lossy qubit array,” Department of Physics Seminar (online), IIT Bombay, November 25, 2020.
- “Long-range coherence and multiple steady states in a lossy qubit array,” Center for Theory of Quantum Matter (CTQM) presentation (online), University of Colorado Boulder, November 9, 2020.
- “Density Matrix Renormalisation Group for continuous systems,” DesOEQ talks (online), University of Cambridge, October 28, 2020.
- “Density Matrix Renormalisation Group for continuous systems,” Quantum 2020 (online), University of Cambridge, October 19, 2020.
- “Long-range coherence and multiple steady states in a lossy qubit array,” Photon 2020 (online) [video], University of Cambridge, September 2, 2020.
- “Long-range entanglement and multistability in a lossy qubit array,” Collective Phenomena Group Meeting (CPGM) talk (online), University of Cambridge, July 21, 2020.
- “Long-range coherence and multiple steady states in a lossy qubit array,” DesOEQ talks (online), University of Cambridge, May 13, 2020.
- 2019
- “Critical Response of a Quantum van der Pol Oscillator,” Centre for Condensed Matter Theory (CCMT) Seminar, Indian Institute of Science (IISc), December 11, 2019.
- “Critical Response of a Quantum van der Pol Oscillator,” Joint DesOEQ-QSUM meeting, University of Oxford, September 16, 2019.
- “Critical Response of a Quantum van der Pol Oscillator,” Collective Phenomena Group Meeting (CPGM) talk, University of Cambridge, July 16, 2019.
- “Critical Response of a Quantum van der Pol Oscillator,” Condensed Matter and Quantum Materials (CMQM) Conference, University of St Andrews, July 03, 2019.
- “Paving an enlightened path to anyons and quantum computation,” Science Lunchtime Seminar, Darwin College, Cambridge, April 25, 2019.
- “Creating and Braiding Anyons in an Optical Cavity,” Department of Physics Seminar, University of Strathclyde, January 2019.
- 2018
- “Creating and Braiding Anyons in an Optical Cavity,” Collective Phenomena Group Meeting (CPGM) talk, University of Cambridge, October 10, 2018.
- “Creating and Braiding Anyons in an Optical Cavity,” Public talk (thesis defense), Department of Physics, Cornell University, April 27, 2018.
- 2017
- “Collective Dynamics of Solitons in Superfluids,” Research highlight for prospective graduate students, Department of Physics, Cornell University, March 27, 2017.
Posters
- 2022
- “Controllable long-range entanglement of lossy qubits,” Openness as a resource (OpenQ22) workshop, MPIPKS, Dresden, Germany, February 1, 2022.
- 2021
- “Symmetry-Protected Long-Range Entanglement in a Lossy Qubit Array,” BEC 2021 (online), Sant Feliu de Guixols, Spain, September 15, 2021.
- “Pulsed generation of symmetry-protected nonlocal Bell pairs,” Quantum Optics X (online), Toruń, Poland, September 6, 2021.
- “Density-Matrix Renormalization Group for Continuous Quantum Systems,” QuAMP 2021 (online), September 1, 2021.
- “Pulsed Generation of Symmetry-Protected Long-Range Entanglement,” QuAMP 2021 (online), August 21, 2021.
- 2020
- “Long-range coherence and multistability of lossy qubits,” Munich Conference on Quantum Science and Technology (MCQST), Cambridge (online), UK, July 6, 2020.
- 2019
- “Critical Response of a Quantum van der Pol Oscillator,” Bose-Einstein Condensation (BEC) 2019, Sant Feliu de Guixols, Spain, September 9, 2019.
- “Creating and Braiding Anyons in an Optical Cavity,” MPIPKS International Workshop on Synthetic Topological Matter, Dresden, Germany, May 21, 2019.
- “Critical Response of a Quantum van der Pol Oscillator,” DesOEQ (Designing Out-of-Equilibrium Quantum systems) Review Meeting, Glasgow, Scotland, March 14, 2019.
- 2018
- “Creating and Braiding Anyons in an Optical Cavity,” DesOEQ Annual Meeting & DOQS Workshop, Glasgow, Scotland, October 15, 2018.
- “Creating and Braiding Anyons in an Optical Cavity,” 49th Annual Meeting of the APS Division of Atomic, Molecular and Optical Physics (DAMOP), Fort Lauderdale, Florida, May 30, 2018.
- “Creating and Braiding Anyons in an Optical Cavity,” Cornell Center for Materials Research (CCMR) Symposium on Advances in Photonics and Quantum Optics, Ithaca, New York, May 23, 2018.
- 2017
- “Creating and Braiding Anyons in an Optical Cavity,” ARO/AFOSR Quantum Matter MURI Program Review, Gaithersburg, Maryland, October 12, 2017.
- “Creating and Braiding Anyons in an Optical Cavity,” ITAMP workshop on Many-Body Cavity QED, Boston, Massachusetts, October 10, 2017.
- “Collective Modes of a Soliton Train in a Fermi Superfluid,” 48th Annual Meeting of the APS Division of Atomic, Molecular and Optical Physics (DAMOP), Sacramento, California, June 6, 2017.
- 2016
- “Collective Modes of a Soliton Train in a Fermi Superfluid,” ARO/AFOSR Quantum Matter MURI Program Review, Chicago, Illinois, September 27, 2016.
Public engagement
-
News articles and research highlights written for a general audience:
- Surprising nature of quantum solitary waves revealed
- Researchers pave an enlightened path to anyons and quantum computation
- A quantum ear
- Hidden symmetry could be key to more robust quantum systems, researchers find
- Entangled quantum bits protected by symmetry
- Towards quantum simulation of false vacuum decay
- Towards table-top quantum simulation of vacuum decay
- Mutating Quantum Particles Set in Motion
- Particles that mutate by moving from place to place
- DMRG for quantum systems in the continuum
- Seminar for non-physicists: Paving an enlightened path to anyons and quantum computation.
- Non-technical summary and illustrations here (see above) and on Cambridge website.
- Judge in the National Finals for the 2022 Raman Awards.
- Short presentations on YouTube channel.
Unpublished work
- Understanding a long-standing puzzle in liquid Helium-3: How does the superfluid B phase nucleate in the supercooled liquid? (2018) [with Erich Mueller and Jeevak Parpia].
Click here to read more!
Cut a long story (see below) short: the puzzle is still open as ever! We tried sophisticated approaches for finding the nucleation energy, such as the nudged elastic band method, but that did not explain the observations.
Helium is one of the few elements which refuses to solidify at normal pressure no matter how much it is cooled. This is a consequence of the Heisenberg uncertainty principle of quantum mechanics which prevents everything from coming to a standstill even at absolute zero temperature. The residual energy, called the zero-point energy, is larger for lighter elements like Helium. Moreover, being a noble gas, the interatomic forces in helium are weak — too weak, in fact, to lock the atoms into a regular grid and form a solid. So it remains a liquid even at absolute zero. But that is only the start – the story gets much more interesting!
There are two stable isotopes of Helium: He-3 and He-4. As early as 1937, He-4 was cooled below a few K, where it suddenly became a superfluid, displaying some bizarre properties! On the other hand, He-3 remained a rather “boring” liquid even at much lower temperatures. But in November 1971, in a cold Ithaca winter (~250 K), He-3 was cooled much further (~2 mK), and lo! It turned superfluid. Not only that, two different types of superfluid — called rather unimaginatively “A” and “B” 🙂 . This vast difference between the two isotopes has its origin in quantum statistics. He-4 has an even number of fermions (protons, neutrons, and electrons), so it obeys Bose statistics. Conversely, He-3 has an odd number of fermions and obeys Fermi statistics. And that makes all the difference. Whereas bosons can condense into the same state at low temperatures, fermions have to pair up before they can condense. This Cooper pairing occurs at much lower temperatures, and depending on the internal structure of the pairs, He-3 can form different superfluid states which are much more exotic than the structureless superfluid of He-4! Read this entertaining review.
Now comes the puzzle: the superfluid A phase is stable only above a critical temperature, below which the superfluid B phase is stable (see phase diagram). However, He-3 can be “supercooled” below this critical temperature and still remain in the A phase. Now, the puzzle comes in how the liquid eventually turns into the B phase as it is cooled further. Experiments have seen such nucleation of the B phase, but we still don’t understand the mechanism! Despite some rather crazy proposals, there is yet no definitive theoretical understanding which explains this nucleation phenomena. However, new experiments underway in Jeevak Parpia’s lab at Cornell.
- 1D-to-3D crossover in the superfluidity of a spin-imbalanced Fermi gas in an array of coupled tubes (2016) [with Erich Mueller].
Click here to read more!
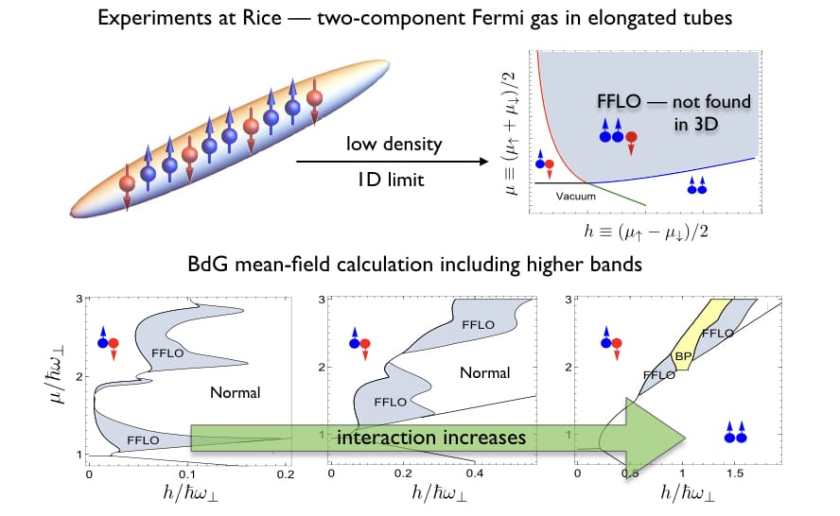
This is an extension of our work on dimensional crossover in a cylindrically confined spin-imbalanced Fermi gas (see above). Here we consider a 3D gas broken up into tubes by a 2D lattice, as in experiments at Rice, and calculate the (BdG) phase diagram taking into account the higher energy bands. The 1D-to-3D crossover occurs in two different manner depending on whether the lattice depth is decreased or the interactions are increased. For weak interactions, when the (average) chemical potential lies within an energy band, we find 3D-like behavior, whereas if the chemical potential lies between the 1st and 2nd band, we find 1D like behavior. As the lattice depth is decreased, these features are qualitatively unchanged, however the energy bands get wider and eventually the spectrum becomes gapless, making the entire phase diagram 3D like. On the other hand, stronger interactions cause mixing between the energy bands and the 1D-like behavior is suppressed.
-
Note: In the figures, gray regions indicate locations of the energy bands. Some of the figures only show the critical imbalance for the BCS state. Generically the region just outside is FFLO. The curve has a positive slope in 3D and a negative slope in 1D.
- Thermalization in a quasi-one-dimensional quantum gas (2015) [with Erich Mueller and Mukund Vengalattore] [manuscript] [slides].
Click here to read more!
We model thermalization in a quantum gas via binary elastic collisions after the gas is loaded into an array of weakly-coupled 1D tubes by turning on an optical lattice in the transverse plane. When the lattice is turned on adiabatically (slow compared to the collision rate), the quasimomentum distribution evolves smoothly into a thermal profile. For small intertube coupling J, the rate of thermalization grows as J2 log J. We show that the equilibration times in two recent experiments [Nature 467, 567 (2010)] and [Nature 440, 900 (2006)] differ hugely from one another, which explains why one of them saw a thermal cloud whereas the other didn’t. When the lattice is turned on suddenly (fast compared to the collision rate), the momentum distribution develops multiple isolated peaks which eventually merge into a thermal distribution. These nonequilibrium peaks originate from the exchange of particles between different energy bands and can be resolved for about 50 collision times.
Undergraduate research
- Bifurcation in classical dynamical systems [with Subhankar Ray]: Explored feature-rich bifurcations in nonlinear systems, focusing on a bead on a rotating hoop [arXiv’11, arXiv’12] and circuit realizations [IEEE’11]; developed techniques for constructing trapping regions to determine the nature of fixed points where linear stability analysis fails.
- Random walks [with Subhankar Ray and Jaya Shamanna]: Used integro-differential equations to model a continuous-time random walk under an external field, modelling subdiffusive transport; formulated recurrence relations for the moments, leading to analytic solutions for a time-dependent jump probability [arXiv’12].
- Photoemission from thin films [with Manas Bose and Chayanika Bose]: Used quantum Boltzmann rate equations to model photocurrent from a semiconductor film as a function of the film thickness and the frequency and polarisation of incident light (final-year project).
- Liquid-gas phase transition of nuclear matter [with Subhankar Ray and Jaya Shamanna]: Used the Bethe-Peierls approximation to model a liquid-gas phase transition in a cubic lattice gas model of cold nuclear matter.
- PT-symmetric quantum mechanics [with Subhankar Ray]: Explored the properties of a class of non-Hermitian Hamiltonians that are symmetric under spacetime reflection, and studied their equivalence to Hermitian Hamiltonians used in ordinary quantum mechanics.
Other activities
- Editorial: Referee for Physical Review Letters (since 2017), Physical Review A (since 2018), and Physical Review B (since 2019).
- Administrative: Co-organizer for the Cavendish Quantum Colloquia 2018-19, University of Cambridge.
- Teaching: Served as teaching assistant, supervisor, or co-instructor for several undergraduate courses at Cornell and Cambridge. Please see the Teaching page for details.